kbsoo

Monty Hall Problem

1

원래도 몬티-홀 문제를 알고는 있었지만 최근에 책을 읽는데 거기에 몬티-홀 문제가 나옴 “n값을 크게 해서 직접 실행해보고 싶다"는 생각이 들었음

아래 글이랑 똑같은 내용이지만 github에도 올렸으니 참고하실 분은 참고하시길

코드

import random
import matplotlib.pyplot as plt

def monty_hall(n):
    switch_wins = 0  # 문을 바꿔서 이긴 횟수
    stay_wins = 0    # 문을 유지해서 이긴 횟수

    for _ in range(n):
        # 자동차가 있는 문을 무작위로 설정 (0, 1, 2 중 하나)
        car = random.randint(0, 2)
        # 참가자가 문을 무작위로 선택 (0, 1, 2 중 하나)
        choice = random.randint(0, 2)

        # 사회자가 염소가 있는 문을 열음
        # 참가자가 선택하지 않은 문 중 자동차가 없는 문을 찾기
        possible_doors = []  # 빈 리스트를 만들어서 조건에 맞는 문을 추가
        for door in range(3):
            if door != choice and door != car:
                possible_doors.append(door)
        
        # 사회자가 열 문을 선택
        if possible_doors:  # possible_doors가 비어있지 않으면
            monty_opens = random.choice(possible_doors)
        else:
            # 참가자가 자동차를 선택한 경우, 나머지 문 중 하나를 무작위로 열음
            remaining_doors = []  # 빈 리스트를 만들어서 조건에 맞는 문을 추가
            for door in range(3):
                if door != choice:
                    remaining_doors.append(door)
            monty_opens = random.choice(remaining_doors)

        # 문을 바꾸는 경우: 참가자가 선택하지 않았고 사회자가 열지 않은 문을 찾기
        switch_choice = None  # 아직 선택된 문이 없음을 표시
        for door in range(3):
            if door != choice and door != monty_opens:
                switch_choice = door
                break  # 문을 하나 찾았으면 반복문 종료
        
        # 문을 바꿔서 이겼는지 확인
        if switch_choice == car:
            switch_wins += 1

        # 문을 유지해서 이겼는지 확인
        if choice == car:
            stay_wins += 1

    return switch_wins, stay_wins

n = 100000000  # 1억 번
switch_wins, stay_wins = monty_hall(n)

# 결과 출력
print(f"문을 바꾸는 전략으로 자동차를 얻은 횟수: {switch_wins}")
print(f"문을 유지하는 전략으로 자동차를 얻은 횟수: {stay_wins}")
print(f"문을 바꾸는 전략의 승률: {switch_wins / num_trials:.4f}")
print(f"문을 유지하는 전략의 승률: {stay_wins / num_trials:.4f}")

# 시각화
labels = ['Switch', 'Stay']
wins = ****[switch_wins, stay_wins]
plt.bar(labels, wins, color=['blue', 'green'])
plt.ylabel('Number of Wins')
plt.title('Monty Hall Problem Simulation (100M Trials)')
plt.show()

# 문을 바꾸는 전략으로 자동차를 얻은 횟수: 66663787
# 문을 유지하는 전략으로 자동차를 얻은 횟수: 33336213
# 문을 바꾸는 전략의 승률: 0.6666
# 문을 유지하는 전략의 승률: 0.3334

2

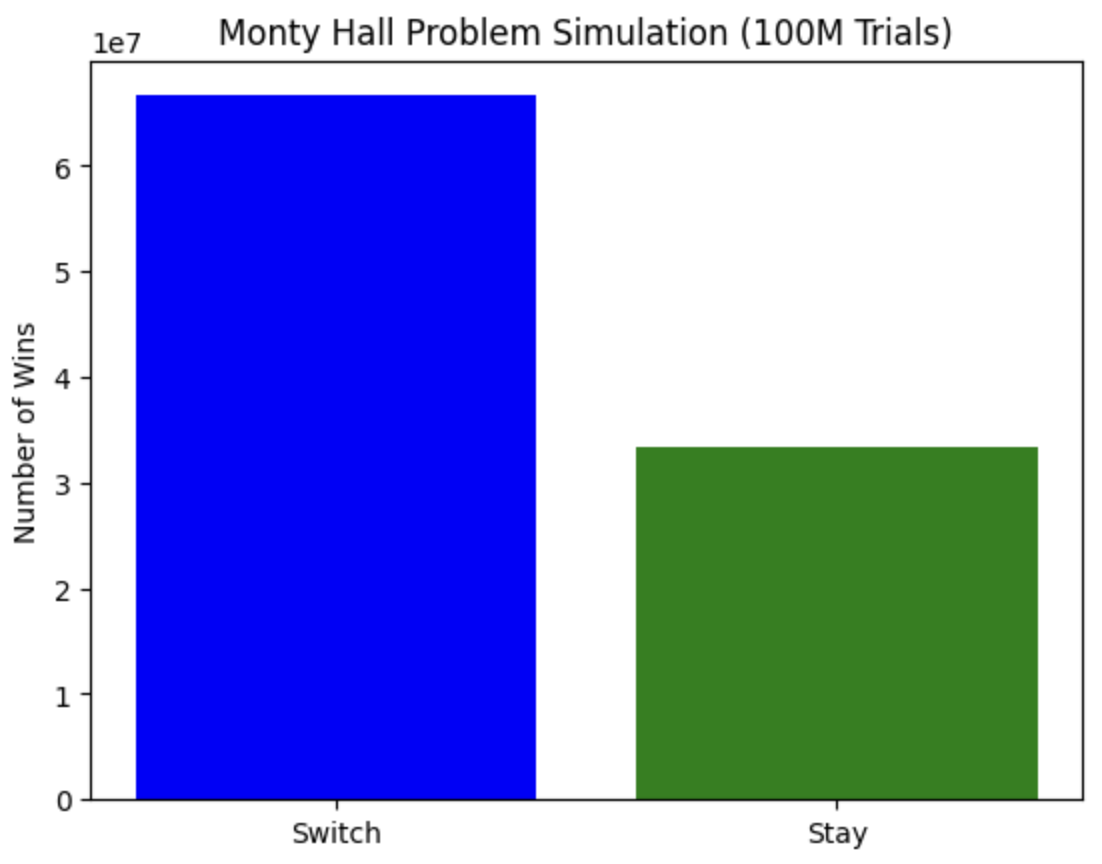
이렇게 결과가 나왔다 바꾸는게 유리하다

자 이제 확률적으로도 맞는지 한번 검증을 해보겠음

베이즈 정리

몬티 홀 문제의 설정

참가자가 문을 바꾸면 자동차를 얻을 확률이 높아질까?

베이즈 정리의 공식

베이즈 정리는 사후 확률을 계산하는 데 사용됨 $P(A|B) = \frac{P(B|A)\times P(A)}{P(B)}$

사건 정의

문제를 구체적으로 풀기 위해 가정하면:

이제 알고 싶은 것

사건 설정

즉, 사회자가 문2를 열었을 때 자동차가 문1에 있을 확률

1. 사전 확률 $P(A)$

자동차는 처음에 세 개의 문 중 하나에 무작위에 배치되므로: $P(A) = P(자동차가 문1에 있음) = \frac{1}{3}$

2. 우도 $P(B|A)$

$P(B|A)$는 자동차가 문1에 있을 때 사회자가 문2를 열 확률

3. 전체 확률 $P(B)$

$P(B)$는 사회자가 문2를 열 확률. 이는 자동차의 위치에 따라 달라지므로, 전체 확률의 법칙을 사용해 계산: $P(B) = P(B|A) \times P(A) + P(B|자동차가 문2에 있음) \times P(자동차가 문2에 있음)$ $ + P(B|자동차가 문3에 있음) \times P(자동차가 문3에 있음)$

각 경우를 계산해보면

  1. 자동차가 문1에 있을 때:
  1. 자동차가 문2에 있을 때:
  1. 자동차가 문3에 있을 때:

이제 전체 확률을 합산하면: $P(B) = \frac{1}{6} + 0 + \frac{1}{3} = \frac{1}{6} + \frac{2}{6} = \frac{3}{6} = \frac{1}{2}$

4. 사후 확률 $P(A|B)$ 계산

이제 베이즈 정리를 사용해 $P(A|B)$를 구함: $P(A|B) = \frac{P(B|A)\times P(A)}{P(B)} = \frac{(\frac{1}{2}) \times (\frac{1}{3})}{\frac{1}{2}} = \frac{\frac{1}{6}}{\frac{1}{2}} = \frac{1}{6} \times 2 = \frac{1}{3}$

따라서 사회자가 문2를 열었을 때 자동차가 문1에 있을 확률은 $\frac{1}{3}$

자동차가 문3에 있을 확률

자동차는 문1 또는 문3에만 있을 수 있음 (문2는 염소가 있음),

따라서 자동차가 문3에 있을 확률은:

$P(자동차가 문3에 있음|B) = 1 - P(A|B) = 1 - \frac{1}{3} = \frac{2}{3}$

결론

이렇게 코드로 돌려본 것과 확률적으로 일치함을 알 수 있었음!